本题其实就是最短路的延伸版本，如果不了解最短路的可以看我这篇文章：【笔记】图论-最短路径算法。

如果了解最短路的一定知道， Bellman-Ford 算法是可以判断负环的，方法也很简单，就是在两重循环结束后再遍历每一条边（下文通称称这条边的起点为点uu，终点为点vv），如果从点uu到点vv比disvdis_v还要短，那么就存在负环。

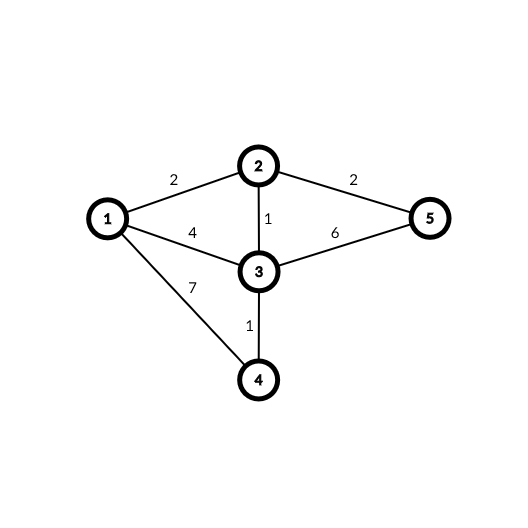
为什么呢？我们来看下面这张图：

假设从点 1 出发，手动模拟一下 Bellman-ford 的两重循环可以算出：dis1=−2,dis2=−1,dis3=1dis_1=-2,dis_2=-1,dis_3=1，但此时，很明显可以看出，从点33到点11为−3-3，比dis1dis_1还要小，所以此时是存在负环的。

因为如果存在负环，那么每在环中转一圈，就会减小一定的值，这样就不存在最短路了，不论你转多少圈，再转一圈始终会比当前的最短距离短，如果不存在负环，那么最短路就是确定的，也就是说经过n×mn\times m次循环一定能求出最短的路径。

根据以上思路，我打出了一段代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
#include<bits/stdc++.h>
using namespace std;
int t,n,m,k,u[6001],v[6001],c[6001],dis[2001];//因为有可能全都是双向边，所以数组要开成 m 的两倍
int main()
{
	scanf("%d",&t);
	while(t--)
	{
		memset(dis,0x3f3f3f,sizeof(dis));
		k=0;
		scanf("%d%d",&n,&m);
		for(int i=1;i<=m;i++)
		{
			k++;
			scanf("%d%d%d",&u[k],&v[k],&c[k]);//Bellman-Ford 这样存边更方便
			if(c[k]>=0)
			{
				k++;
				u[k]=v[k-1];
				v[k]=u[k-1];
				c[k]=c[k-1];
			}
		}
		dis[1]=0;
		for(int i=1;i<=n;i++)
			for(int j=1;j<=k;j++)//Bellman-Ford 朴素算法
				dis[v[j]]=min(dis[v[j]],dis[u[j]]+c[j]);
		for(int i=1;i<=k;i++)
			if(dis[v[i]]>dis[u[i]]+c[i])//判断负环
			{
				printf("YE5\n");//毒瘤出题人解释一下为什么是 YE5！！！
				goto l;//懒得写 flag，直接跳出循环到 l: 处
			}
		printf("N0\n");
		l:;
	}
	return 0;
}

如果你看到上面这段代码就很高兴地回去改了，那么很遗憾地告诉你，这是 90pts 的代码。

为什么呢？我们看题目：

寻找一个从顶点11所能到达的负环。

上面那段代码判断的是有没有负环，但题目要求是求从点11能到的负环，所以会错。

什么意思呢？意思是从点11开始，要能到这个负环才行，如果点11与这个负环不连通，那么就还是输出N0。

怎么改呢？很简单，用一个bb数组表示每个点能否从点11到达，就像 Dijkstra 一样，枚举每条边时，我们判断一下这条边的出发点是否能从点11到达就行了，如果出发点目前不能从点11到达，就不管这条边，如果可以，就把这条边的终点也标记为可以从点11到达。同时，最后在判断负环时，也要判断当前边的出发点是否能从点11到达。这样不能从点11到达的负环就不会被判断到了。

那么，这么做会不会影响disdis数组的更新呢？当然不会，我们本来就是为了避免误将没有更新过的点当成已更新过的，才会把disdis数组设成无穷大的，现在只是另开了一个数组来代替这个功能而已。

还是比较简单吧，加了几行代码而已：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
#include<bits/stdc++.h>
using namespace std;
int t,n,m,k,u[6001],v[6001],c[6001],dis[2001],b[2001];
int main()
{
	scanf("%d",&t);
	while(t--)
	{
        memset(b,0,sizeof(b));
		k=0;
		scanf("%d%d",&n,&m);
		for(int i=1;i<=m;i++)
		{
			k++;
			scanf("%d%d%d",&u[k],&v[k],&c[k]);
			if(c[k]>=0)
			{
				k++;
				u[k]=v[k-1];
				v[k]=u[k-1];
				c[k]=c[k-1];
			}
		}
		dis[1]=0;
		b[1]=1;
		for(int i=1;i<=n;i++)
			for(int j=1;j<=k;j++)
				if(b[u[j]])
				{
					dis[v[j]]=min(dis[v[j]],dis[u[j]]+c[j]);
					b[v[j]]=1;
				}
		for(int i=1;i<=k;i++)
			if((b[u[i]]||b[v[i]])&&dis[v[i]]>dis[u[i]]+c[i])
			{
				printf("YE5\n");
				goto l;
			}
		printf("N0\n");
		l:;
	}
	return 0;
}

好了，没有套路了，这就是 AC 的代码。

评测记录：

Bellman-Ford 真香。